Skip to content

Number Systems

Introduction to Number Systems

A number system is a systematic way to represent numbers with symbolic characters and uses a base value to conveniently group numbers in a compact form. The base of a number system is also called its radix. It is the total number of distinct symbols or digits used to represent numbers in that system.

In any number system, the value of a digit depends on its position within the number. This is known as positional notation. The value is determined by the digit itself, its position in the number, and the base of the system.

The value of a number can be expressed as a sum of products of each digit with the base raised to the power of its position. For a number with digits \(d_n d_{n-1} ... d_1 d_0 . d_{-1} d_{-2} ... d_{-m}\), its value \(V\) in base \(b\) is:

\[ V = \sum_{i=-m}^{n} (d_i \times b^i) \]

Where \(d_i\) is the digit at position \(i\).

Types of Number Systems

Decimal Number System

The decimal number system is the most common number system used in our daily lives.

  • Base (Radix): 10
  • Digits Used: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
  • Positional Values: Powers of 10 (\(10^0, 10^1, 10^2, \dots\)).

Example: \( (452.73)_{10} \)

The number \(452.73\) in decimal can be represented as:

\[ (4 \times 10^2) + (5 \times 10^1) + (2 \times 10^0) + (7 \times 10^{-1}) + (3 \times 10^{-2}) \]
\[ = (4 \times 100) + (5 \times 10) + (2 \times 1) + (7 \times 0.1) + (3 \times 0.01) \]
\[ = 400 + 50 + 2 + 0.7 + 0.03 = 452.73 \]

Binary Number System

The binary number system is the fundamental language of computers. It uses only two digits. Each digit is called a bit (binary digit).

  • Base (Radix): 2
  • Digits Used: 0, 1
  • Positional Values: Powers of 2 (\(2^0, 2^1, 2^2, \dots\)).

Example: \( (1101.101)_2 \)

The number \(1101.101\) in binary can be converted to decimal as:

\[ (1 \times 2^3) + (1 \times 2^2) + (0 \times 2^1) + (1 \times 2^0) + (1 \times 2^{-1}) + (0 \times 2^{-2}) + (1 \times 2^{-3}) \]
\[ = (1 \times 8) + (1 \times 4) + (0 \times 2) + (1 \times 1) + (1 \times 0.5) + (0 \times 0.25) + (1 \times 0.125) \]
\[ = 8 + 4 + 0 + 1 + 0.5 + 0 + 0.125 = (13.625)_{10} \]

Octal Number System

The octal number system is often used in computing as a more compact way to represent binary numbers.

  • Base (Radix): 8
  • Digits Used: 0, 1, 2, 3, 4, 5, 6, 7
  • Positional Values: Powers of 8 (\(8^0, 8^1, 8^2, \dots\)).

Example: \( (273.5)_8 \)

The number \(273.5\) in octal can be converted to decimal as:

\[ (2 \times 8^2) + (7 \times 8^1) + (3 \times 8^0) + (5 \times 8^{-1}) \]
\[ = (2 \times 64) + (7 \times 8) + (3 \times 1) + (5 \times 0.125) \]
\[ = 128 + 56 + 3 + 0.625 = (187.625)_{10} \]

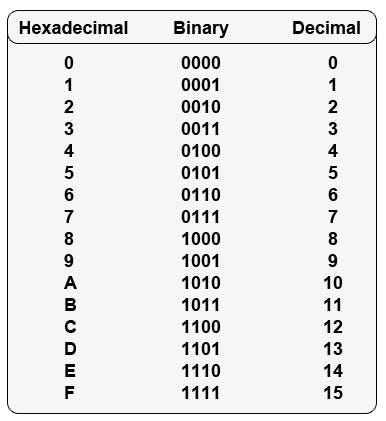
Hexadecimal Number System

The hexadecimal system is widely used in computer systems to represent data like memory addresses and colors. It's even more compact than octal.

  • Base (Radix): 16
  • Digits Used: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
    • Where A=10, B=11, C=12, D=13, E=14, F=15.
  • Positional Values: Powers of 16 (\(16^0, 16^1, 16^2, \dots\)).

Example: \( (1A5.C)_{16} \)

The number \(1A5.C\) in hexadecimal can be converted to decimal as:

\[ (1 \times 16^2) + (A \times 16^1) + (5 \times 16^0) + (C \times 16^{-1}) \]
\[ = (1 \times 256) + (10 \times 16) + (5 \times 1) + (12 \times 0.0625) \]
\[ = 256 + 160 + 5 + 0.75 = (421.75)_{10} \]

Number System Conversions

Decimal to Other Bases

To convert a decimal number to another base, we handle the integer and fractional parts separately.

Integer Part Conversion

Use the repeated division method.

  1. Divide the decimal number by the target base.
  2. Record the remainder.
  3. Replace the number with the quotient from the division.
  4. Repeat steps 1-3 until the quotient is 0.
  5. The new number is the sequence of remainders read from bottom to top.

Convert \( (43)_{10} \) to Binary

Division Quotient Remainder
\(43 \div 2\) 21 1 (LSB)
\(21 \div 2\) 10 1
\(10 \div 2\) 5 0
\(5 \div 2\) 2 1
\(2 \div 2\) 1 0
\(1 \div 2\) 0 1 (MSB)

Reading the remainders from bottom to top, we get \(101011\). So, \( (43)_{10} = (101011)_2 \).

Fractional Part Conversion

Use the repeated multiplication method.

  1. Multiply the fractional part of the decimal number by the target base.
  2. Record the integer part of the result.
  3. Replace the fractional part with the fractional part of the result.
  4. Repeat steps 1-3 until the fractional part becomes 0 or you reach the desired precision.
  5. The new fractional number is the sequence of integers read from top to bottom.

Convert \( (0.625)_{10} \) to Binary

Multiplication Result Integer Part
\(0.625 \times 2\) 1.25 1 (MSB)
\(0.25 \times 2\) 0.50 0
\(0.50 \times 2\) 1.00 1 (LSB)

Reading the integer parts from top to bottom, we get \(.101\). So, \( (0.625)_{10} = (0.101)_2 \).

Other Bases to Decimal

To convert a number from any base to decimal, use the positional notation method (also called polynomial expansion).

  1. Multiply each digit by the base raised to the power of its position.
  2. Sum up all the products.

Convert \( (1101)_2 \) to Decimal

\[ (1101)_2 = (1 \times 2^3) + (1 \times 2^2) + (0 \times 2^1) + (1 \times 2^0) \]
\[ = 8 + 4 + 0 + 1 = (13)_{10} \]

Convert \( (345)_8 \) to Decimal

\[ (345)_8 = (3 \times 8^2) + (4 \times 8^1) + (5 \times 8^0) \]
\[ = (3 \times 64) + (4 \times 8) + (5 \times 1) = 192 + 32 + 5 = (229)_{10} \]

Convert \( (A2F)_{16} \) to Decimal

\[ (A2F)_{16} = (A \times 16^2) + (2 \times 16^1) + (F \times 16^0) \]
\[ = (10 \times 256) + (2 \times 16) + (15 \times 1) = 2560 + 32 + 15 = (2607)_{10} \]

Conversions Between Binary, Octal, and Hexadecimal

These conversions are straightforward due to their base relationships (\(8 = 2^3\) and \(16 = 2^4\)).

Binary to Octal

Group binary digits into sets of three, starting from the binary point. Add leading or trailing zeros if needed. Convert each group to its octal equivalent.

Convert \( (10110101)_2 \) to Octal

  1. Group the bits into threes from right to left: \( \underline{10} \quad \underline{110} \quad \underline{101} \)
  2. Add a leading zero to the first group to make it three bits: \( \underline{010} \quad \underline{110} \quad \underline{101} \)
  3. Convert each group:
    • \( (010)_2 = (2)_8 \)
    • \( (110)_2 = (6)_8 \)
    • \( (101)_2 = (5)_8 \)
  4. Combine the results: \( (265)_8 \). So, \( (10110101)_2 = (265)_8 \).
Octal to Binary

Convert each octal digit to its 3-bit binary equivalent.

Convert \( (724)_8 \) to Binary

  1. Convert each octal digit:
    • \( (7)_8 = (111)_2 \)
    • \( (2)_8 = (010)_2 \)
    • \( (4)_8 = (100)_2 \)
  2. Combine the results: \( (111010100)_2 \). So, \( (724)_8 = (111010100)_2 \).
Binary to Hexadecimal

Group binary digits into sets of four, starting from the binary point. Add leading or trailing zeros if needed. Convert each group to its hexadecimal equivalent.

Convert \( (110101101011)_2 \) to Hexadecimal

  1. Group the bits into fours from right to left: \( \underline{1101} \quad \underline{0110} \quad \underline{1011} \)
  2. Convert each group:
    • \( (1101)_2 = (13)_{10} = (D)_{16} \)
    • \( (0110)_2 = (6)_{10} = (6)_{16} \)
    • \( (1011)_2 = (11)_{10} = (B)_{16} \)
  3. Combine the results: \( (D6B)_{16} \). So, \( (110101101011)_2 = (D6B)_{16} \).
Hexadecimal to Binary

Convert each hexadecimal digit to its 4-bit binary equivalent.

Convert \( (9AF)_16 \) to Binary

  1. Convert each hex digit:
    • \( (9)_{16} = (1001)_2 \)
    • \( (A)_{16} = (1010)_2 \)
    • \( (F)_{16} = (1111)_2 \)
  2. Combine the results: \( (100110101111)_2 \). So, \( (9AF)_{16} = (100110101111)_2 \).
Octal to Hexadecimal (and Vice Versa)

The easiest way is to use binary as an intermediate step.

  • Octal to Hexadecimal: Convert the octal number to binary, then regroup the binary bits into sets of four and convert to hexadecimal.
  • Hexadecimal to Octal: Convert the hexadecimal number to binary, then regroup the binary bits into sets of three and convert to octal.

Convert \( (275)_8 \) to Hexadecimal

  1. Octal to Binary:
    • \( (2)_8 = 010 \)
    • \( (7)_8 = 111 \)
    • \( (5)_8 = 101 \)
    • Combined Binary: \( (010111101)_2 \)
  2. Binary to Hexadecimal:
    • Regroup into fours from the right: \( \underline{0000} \quad \underline{1011} \quad \underline{1101} \)
    • Correct grouping: \( \underline{1011} \quad \underline{1101} \). We have \( (010111101)_2 \). So, \( \underline{0}10111101 \rightarrow \underline{0001} \quad \underline{0111} \quad \underline{1101} \)
    • Wait, let's re-do the binary grouping carefully. Binary is \(010111101\).
    • Group from right: \( \underline{01011} \quad \underline{1101} \). No. It's \( \underline{010} \quad \underline{111} \quad \underline{101} \). Binary: 010111101.
    • Regroup from right in fours: 01011 1101. No, that's not right. 010 111 101. The full binary string is 010111101.
    • Grouping from the right: 1101 and 01011. That's not right either.
    • Let's regroup 010111101 from the right in groups of 4:
    • 1101 (rightmost group)
    • 0111 (middle group)
    • 0 (leftmost group, needs padding) -> 0000 -> 0. Let's use 1.
    • Binary: \( \underline{0001} \quad \underline{0111} \quad \underline{1101} \)
    • The binary is 010111101. So from the right: 1101 is one group. 0101 is the second. 1 is left over.
    • \( \underline{1} \quad \underline{0111} \quad \underline{1101} \). Let's re-check the octal->binary. \(2 \rightarrow 010, 7 \rightarrow 111, 5 \rightarrow 101\). Binary: \(010111101\). OK.
    • Regroup \(010111101\) in fours from the right: \( \underline{1101} \) (is D), \( \underline{0101} \) (is 5), left with \( \underline{1} \). Pad to \( \underline{0001} \) (is 1).
    • So, \( \underline{0001} \quad \underline{0101} \quad \underline{1101} \)
    • \( (0001)_2 = (1)_{16} \)
    • \( (0101)_2 = (5)_{16} \)
    • \( (1101)_2 = (D)_{16} \)
  3. Result: \( (15D)_{16} \) So, \( (275)_8 = (15D)_{16} \).

Computer Fundamentals

Definition and Basic Components of a Computer

A computer is an electronic device that processes data and performs a vast range of tasks by executing a set of instructions. At a fundamental level, all computers consist of two primary elements: hardware and software.

  • Hardware refers to the physical components of a computer system that you can touch and see.
  • Software is a set of instructions, data, or programs used to operate computers and execute specific tasks.

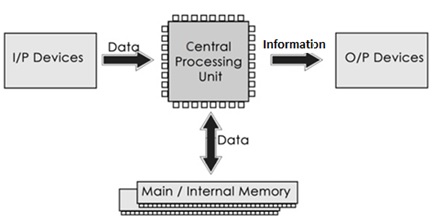
The basic hardware components of a computer include:

Central Processing Unit (CPU)

Often called the "brain" of the computer, the CPU is responsible for executing instructions and performing calculations. It consists of two main parts:

  • Arithmetic Logic Unit (ALT): Performs arithmetic operations (addition, subtraction, etc.) and logical operations (AND, OR, NOT).
  • Control Unit (CT): Directs and coordinates most of the operations in the computer. It interprets instructions and sends signals to other components.

Memory

Memory is where the computer stores data and instructions. There are two main types of memory:

  • Primary Memory (Main Memory): This is the memory that the CPU can access directly. It is volatile, meaning its contents are lost when the computer is turned off.
    • Random Access Memory (RAM): Used to store data and instructions that are currently in use.
    • Read-Only Memory (ROM): Contains pre-written instructions that are essential for booting up the computer.
  • Secondary Memory (Storage): This is non-volatile memory used for long-term storage of data and programs.
    • Hard Disk Drive (HDD): A magnetic storage device.
    • Solid-State Drive (SSD): Uses flash memory for storage, which is much faster than an HDD.
    • Optical Drives: Such as CD/DVD/Blu-ray drives.
    • Flash Memory: Used in USB drives and memory cards.

Input Devices

These devices are used to provide data and control signals to a computer.

  • Keyboard
  • Mouse
  • Scanner
  • Microphone
  • Webcam

Output Devices

These devices are used to display the results of the processed data.

  • Monitor
  • Printer
  • Speakers
  • Projector

Motherboard

The motherboard is the main printed circuit board (PCB) in a computer. It holds and allows communication between many of the crucial electronic components of a system, such as the CPU and memory.

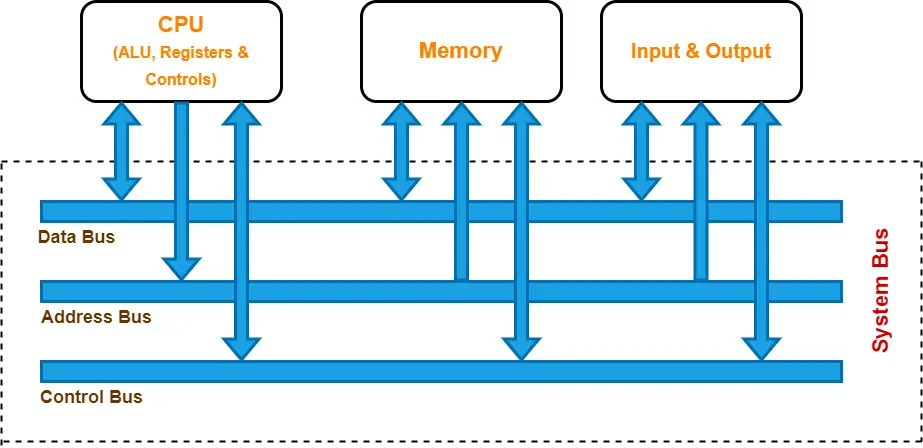
Bus Architecture

In computer architecture, a bus is a communication system that transfers data between components inside a computer, or between computers. It is a set of parallel electrical conductors that can be a path for data, addresses, or control signals.

There are three main types of buses in a computer system:

Address Bus

The address bus is a unidirectional pathway that carries the memory address from the CPU to the main memory or other I/O devices. The width of the address bus determines the maximum amount of memory the system can address. For example, a system with a 32-bit address bus can address \(2^{32}\) memory locations.

Data Bus

The data bus is a bidirectional pathway that carries the actual data between the CPU, memory, and I/O devices. The width of the data bus determines the amount of data that can be transferred at one time.

Control Bus

The control bus is a bidirectional pathway that carries control signals and timing signals to coordinate the activities of all the components. These signals include read/write commands, interrupt requests, and clock signals.

Evolution and Generations of Computers

The evolution of computers is often categorized into generations, with each generation being characterized by a major technological development.

First Generation (1940-1956): Vacuum Tubes

  • Technology: Used vacuum tubes for circuitry and magnetic drums for memory.
  • Characteristics:
    • Very large in size, often taking up entire rooms.
    • Consumed a great deal of electricity and generated a lot of heat.
    • Relied on machine language for programming.
    • Examples: ENIAC, UNIVAC.

Second Generation (1956-1963): Transistors

  • Technology: Transistors replaced vacuum tubes.
  • Characteristics:
    • Smaller, faster, cheaper, and more energy-efficient than first-generation computers.
    • Used assembly language and early high-level programming languages like FORTRAN and COBOL.
    • Still generated a considerable amount of heat.

Third Generation (1964-1971): Integrated Circuits

  • Technology: Integrated circuits (ICs), which are small chips containing hundreds of transistors.
  • Characteristics:
    • Significantly smaller and faster than previous generations.
    • Keyboards and monitors were introduced for user interaction.
    • Used operating systems for the first time, allowing them to run multiple applications at once.

Fourth Generation (1971-Present): Microprocessors

  • Technology: The microprocessor, which integrates all the components of a CPU onto a single chip.
  • Characteristics:
    • Led to the development of personal computers (PCs).
    • More powerful, compact, reliable, and affordable.
    • Development of Graphical User Interfaces (GUIs), the mouse, and handheld devices.

Fifth Generation (Present and Beyond): Artificial Intelligence

  • Technology: Based on Artificial Intelligence (AI), with a focus on parallel processing and superconductors.
  • Characteristics:
    • Aims to develop devices that respond to natural language input and are capable of learning and self-organization.
    • Includes technologies like voice recognition, quantum computing, and nano-technology.

Classification of Computers

Computers can be classified based on their size, purpose, and data handling capabilities.

Classification by Size

  • Supercomputers: The largest and most powerful computers, used for complex scientific and engineering problems.
  • Mainframe Computers: Large, powerful, and expensive computers used by large organizations for critical applications, such as bulk data processing.
  • Minicomputers (Midrange Computers): Smaller than mainframes but larger than microcomputers, often used as servers in a network.
  • Microcomputers (Personal Computers): The most common type of computer, designed for individual use. They include desktops, laptops, and tablets.
  • Workstations: High-end microcomputers with more powerful processors and better graphics capabilities, used for tasks like graphic design and engineering.

Classification by Purpose

  • General-Purpose Computers: Designed to perform a wide variety of tasks. Most computers today are general-purpose.
  • Special-Purpose Computers: Designed to perform a specific task or a limited range of tasks. Examples include computers in cars, washing machines, and ATMs.

Classification by Data Handling

  • Analog Computers: Process analog data, which is continuous in nature. They are used for measuring physical quantities like temperature and pressure.
  • Digital Computers: Process digital data, which is in the form of discrete values (0s and 1s). Most modern computers are digital.
  • Hybrid Computers: Combine the features of both analog and digital computers. They are used in specialized applications where both types of data need to be processed.

Data Representation in Computers

In the digital world, all data—be it text, numbers, images, or sound—is ultimately stored as a series of binary digits, or bits. A bit can only have one of two values: 0 or 1. To represent complex information like human language, computers need standardized systems to map characters to these binary numbers. These systems are called character encodings.

ASCII (American Standard Code for Information Interchange)

ASCII was one of the earliest and most influential character encoding standards, developed in the 1960s. Its primary goal was to provide a standard for representing English characters on teleprinters and computers.

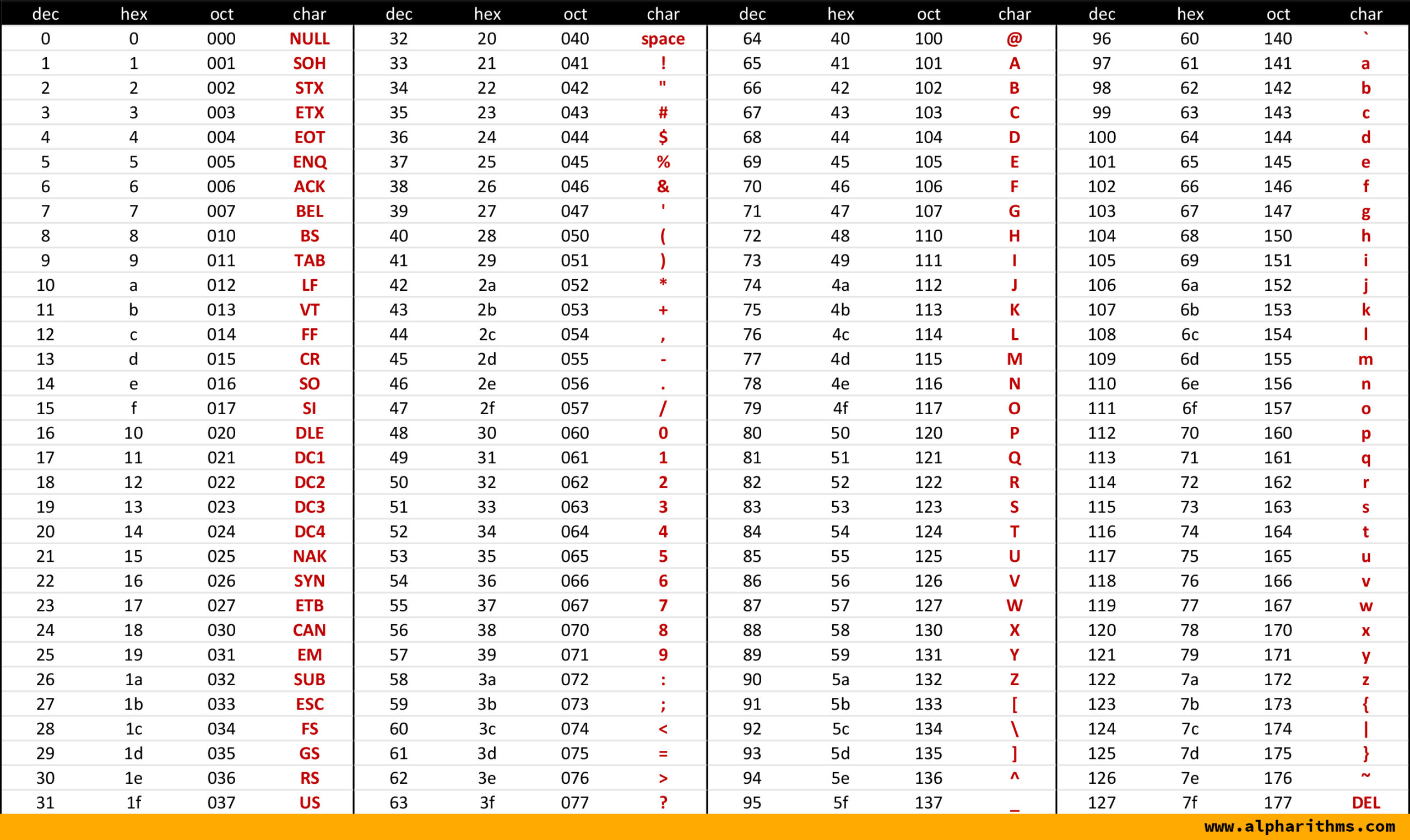
Standard ASCII (7-bit)
  • Structure: Standard ASCII uses 7 bits to represent each character. With 7 bits, it's possible to represent \(2^7 = 128\) unique characters.
  • Character Set: These 128 code points are divided into two main groups:
    1. Control Characters (Codes 0-31 and 127): These are non-printable characters used to control devices. Examples include:
      • NULL (0): Null character
      • BEL (7): Bell (makes a sound)
      • BS (8): Backspace
      • LF (10): Line Feed
      • CR (13): Carriage Return
      • ESC (27): Escape
    2. Printable Characters (Codes 32-126): These are the characters that can be displayed or printed. This set includes:
      • Punctuation marks and symbols (e.g., !, @, #, $)
      • Digits (0 through 9)
      • Uppercase English alphabet (A through Z)
      • Lowercase English alphabet (a through z)
      • Space character (Code 32)

Example: * The uppercase letter 'A' is represented by the decimal number 65, which in 7-bit binary is 1000001. * The digit '5' is represented by the decimal number 53, which in 7-bit binary is 0110101.

Extended ASCII (8-bit)
  • Structure: Since most computers store data in 8-bit chunks (bytes), the 8th bit, which was unused in standard ASCII, was utilized to create Extended ASCII. This allowed for an additional 128 characters, bringing the total to \(2^8 = 256\).
  • Problem of Standardization: The first 128 characters remained the same as standard ASCII. However, there was no single, universally accepted standard for the additional 128 characters (codes 128-255). Different manufacturers and organizations used them for different purposes, such as:
    • Graphical symbols
    • Mathematical symbols
    • Characters from other languages (e.g., accented letters like é, ü).
  • This led to the creation of different code pages (e.g., ISO-8859-1 for Western European languages), which caused compatibility issues. A file created with one code page would not display correctly on a system using a different one.

Unicode

Unicode was created to solve the problems of limited character sets and conflicting code pages. It is a universal character encoding standard designed to support all writing systems in the world, both modern and historical.

Core Concept: Code Points

The fundamental idea behind Unicode is to assign a unique number, called a code point, to every single character. This includes not just letters and numbers but also symbols, punctuation, and even emojis.

  • Notation: Unicode code points are typically written in hexadecimal with a "U+" prefix. For example, U+0041 is the code point for the character 'A'.
  • Planes: The entire range of Unicode code points is divided into 17 "planes," each containing 65,536 ( \(2^{16}\) ) code points.
    • The first plane (Plane 0) is the Basic Multilingual Plane (BMP). It contains code points from U+0000 to U+FFFF and includes most of the commonly used characters from modern languages.
    • The other 16 planes are called supplementary planes and are used for less common characters, historic scripts, and emojis.
Unicode Encoding Schemes

A code point is just an abstract number. An encoding scheme defines how these code points are translated into a sequence of bytes for storage and transmission. The most common Unicode encodings are UTF-8, UTF-16, and UTF-32.

UTF-8 (Unicode Transformation Format - 8-bit)

UTF-8 is the most popular encoding on the web and for many operating systems. * Variable-Width Encoding: It uses a variable number of bytes to represent each character. * 1 byte: For all standard ASCII characters (U+0000 to U+007F). * 2 bytes: For Latin letters with diacritics, Greek, Cyrillic, Hebrew, Arabic, etc. * 3 bytes: For characters in the rest of the BMP (e.g., Chinese, Japanese, Korean). * 4 bytes: For characters in the supplementary planes (e.g., rare characters, most emojis 👍). * Key Advantage: Backward Compatibility: A major reason for its success is that it is 100% backward compatible with 7-bit ASCII. Any text file containing only ASCII characters is also a valid UTF-8 file. This made the transition from ASCII to Unicode much smoother.

UTF-16 (Unicode Transformation Format - 16-bit)
  • Variable-Width Encoding: UTF-16 uses either 2 bytes (16 bits) or 4 bytes (32 bits) per character.
    • It uses 2 bytes for all characters in the BMP.
    • For characters in the supplementary planes, it uses a pair of 2-byte sequences called a surrogate pair.
  • Usage: It is used internally by systems like Microsoft Windows and Java.
UTF-32 (Unicode Transformation Format - 32-bit)
  • Fixed-Width Encoding: UTF-32 is the simplest of the three. It uses a fixed 4 bytes (32 bits) for every single Unicode character.
  • Advantage: Every character has the same length, which can simplify programming tasks like finding the nth character in a string.
  • Disadvantage: It is very space-inefficient. A text file containing only English characters would be four times larger in UTF-32 than in ASCII or UTF-8.

Comparison: ASCII vs. Unicode

Feature ASCII Unicode
Size 7-bit (Standard) or 8-bit (Extended) A standard, not an encoding. Code points up to 21 bits.
Encoding Itself is the encoding. Uses encoding schemes like UTF-8, UTF-16, UTF-32.
Capacity 128 characters (Standard) or 256 (Extended). Over 1.1 million possible code points (currently over 149,000 assigned).
Scope Primarily for the English language. Aims to include every character from every language.
Compatibility Extended ASCII has many conflicting versions (code pages). Provides a single, universal standard. UTF-8 is backward compatible with 7-bit ASCII.
Memory Usage Fixed 1 byte per character. Variable, depending on the encoding and character. UTF-8 is very efficient for English/Latin text.

Problem Set

Number Systems (40 Problems)

Introduction and Core Concepts

  1. Define 'radix' or 'base' of a number system. State the radix for binary, octal, decimal, and hexadecimal systems.
  2. What is the significance of the positional value in a number system? Illustrate with the decimal number \(345\).
  3. Why is the binary system ideal for electronic computers?
  4. List all the valid digits for the base-7 number system.
  5. What is the largest value that can be represented by a single hexadecimal digit? What is its decimal equivalent?
  6. Explain why \(387_8\) is an invalid octal number.
  7. Convert the number \(20_{10}\) into its equivalent in base-2, base-8, and base-16.
  8. Which has a greater value: \(101010_2\) or \(50_{10}\)? Justify your answer.
  9. What is the weight of the digit 'A' in the hexadecimal number \(1AF5_{16}\)?
  10. How many unique numbers can be represented using 8 bits?

Conversions: Decimal to Other Bases

  1. Convert \(428_{10}\) to its binary equivalent.
  2. Convert \(999_{10}\) to its octal equivalent.
  3. Convert \(4096_{10}\) to its hexadecimal equivalent.
  4. Convert the fractional decimal \(0.8125_{10}\) to binary.
  5. Convert \(157.25_{10}\) to its octal equivalent.
  6. Find the hexadecimal equivalent of \(260.5_{10}\).
  7. Convert \(3456_{10}\) to binary.
  8. Convert \(100.1_{10}\) to its binary equivalent (up to 5 fractional places).
  9. Convert \(511_{10}\) to octal.
  10. Convert \(65535_{10}\) to hexadecimal.

Conversions: Other Bases to Decimal

  1. Convert \(11011101_2\) to its decimal equivalent.
  2. Convert \(707_8\) to its decimal equivalent.
  3. Find the decimal value of the hexadecimal number \(F0A1_{16}\).
  4. Convert the binary number \(10110.1101_2\) to decimal.
  5. Convert \(234.5_8\) to its decimal equivalent.
  6. Find the decimal value of \(C4E.B_{16}\).
  7. Convert \(10000001_2\) to decimal.
  8. What is the decimal value of \(BAD_{16}\)?
  9. Convert \(4000_8\) to decimal.
  10. Convert \(1.1_2\) to decimal.

Conversions: Between Binary, Octal, & Hexadecimal

  1. Convert \(101101110111_2\) directly to its octal equivalent.
  2. Convert the octal number \(743_8\) to its binary representation.
  3. Convert \(1111001010100111.101101_2\) directly to its hexadecimal equivalent.
  4. Convert the hexadecimal number \(1ABC.D_{16}\) to its binary representation.
  5. Convert \(652_8\) to hexadecimal. (Hint: First convert to binary).
  6. Convert \(9E7_{16}\) to octal.
  7. Group the bits of \(10111101_2\) to find its octal equivalent.
  8. Convert \(BEEF_{16}\) to binary.
  9. Convert the octal number \(1234_8\) to hexadecimal.
  10. Convert \(A03F_{16}\) to octal.

Computer Fundamentals (40 Problems)

Definition and Basic Components

  1. Draw a neat, labeled block diagram of a computer system. Explain the flow of data between the core components.
  2. Define the CPU. What are the functions of its two main components, the ALU and the CU?
  3. Differentiate between RAM and ROM. Which one is volatile and why?
  4. What is cache memory? Explain its purpose and its position in the memory hierarchy.
  5. List four input devices and four output devices, and state the primary function of each.
  6. What is the role of the motherboard in a computer system?
  7. Explain the fetch-decode-execute cycle performed by the CPU.
  8. What is secondary storage? Provide three examples of secondary storage devices.
  9. Why is a computer referred to as a "system"?
  10. Differentiate between a general-purpose register and a special-purpose register (e.g., Program Counter, Instruction Register).

Bus Architecture

  1. Define 'bus' in computer architecture. What are the three main types of buses in a computer system?
  2. What is the function of the Address Bus? Is it unidirectional or bidirectional? Justify your answer.
  3. If a microprocessor has a 16-bit address bus, what is the maximum memory capacity it can directly address in kilobytes (KB)?
  4. Describe the function of the Data Bus. Why must it be bidirectional?
  5. If a system has a 64-bit data bus, how many bytes of data can be transferred simultaneously?
  6. What is the purpose of the Control Bus? List at least four different control signals it carries.
  7. Explain how the Address, Data, and Control buses work together to perform a write operation to a memory location.
  8. What is bus width? How does the width of the data bus affect the performance of a computer?
  9. Differentiate between a system bus and an expansion bus (like PCI).
  10. What is bus contention and how is it managed?

Evolution and Generations of Computers

  1. What was the defining electronic component for each of the first four generations of computers?
  2. Name two examples of First Generation computers. What were their primary limitations?
  3. How did the shift from vacuum tubes to transistors in the Second Generation improve computers?
  4. What is an Integrated Circuit (IC)? How did its introduction in the Third Generation lead to minicomputers?
  5. The Fourth Generation is defined by the microprocessor. What is a microprocessor and how did it revolutionize the computer industry?
  6. Differentiate between SSI, MSI, LSI, and VLSI in the context of integrated circuits.
  7. What are the primary characteristics and goals of Fifth Generation computers?
  8. What programming languages were characteristic of the First and Second Generations?
  9. How did the user interface evolve from the First Generation (plugs and switches) to the Fourth Generation (GUIs)?
  10. Which generation first saw the widespread use of high-level languages like FORTRAN and COBOL?

Classification of Computers

  1. Classify computers based on size. Briefly describe Supercomputers, Mainframe computers, Minicomputers, and Microcomputers.
  2. What is the primary application area for a supercomputer?
  3. How does a mainframe computer differ from a supercomputer in terms of its processing goals?
  4. Differentiate between a desktop computer, a laptop, and a tablet, which are all types of microcomputers.
  5. Classify computers based on the type of data they process. Explain Analog, Digital, and Hybrid computers.
  6. Provide a real-world example for an analog computer and a hybrid computer.
  7. Classify computers based on their purpose. Differentiate between general-purpose and special-purpose computers with examples.
  8. What is an embedded computer? Give two examples of everyday devices that contain them.
  9. Where does a "server" fit in the classification of computers by size?
  10. What is a workstation, and how does it differ from a standard desktop PC?

Data Representation (20 Problems)

ASCII

  1. What does ASCII stand for? What was its original purpose?
  2. The standard ASCII code is a 7-bit code. What is the total number of characters it can represent?
  3. What is the primary difference between ASCII and Extended ASCII?
  4. The decimal ASCII value for 'a' is 97. What would be the decimal ASCII value for 'e'?
  5. Given that the ASCII code for the character '0' is \(48_{10}\), find the 7-bit binary ASCII code for the character '3'.
  6. What is a major limitation of the ASCII character set in a global context?
  7. Decode the following sequence of 7-bit ASCII codes (in binary): 1001000 1000101 1001100 1001100 1001111.
  8. Are control characters (like newline, tab) part of the ASCII standard?
  9. Explain why ASCII is considered a subset of Unicode's UTF-8.
  10. What happens when a system using Extended ASCII tries to read a file created with a different extended character set (a different code page)?

Unicode

  1. Why was Unicode created? What fundamental problem does it solve?
  2. Explain the difference between a "code point" and an "encoding scheme" in Unicode.
  3. What does UTF in UTF-8, UTF-16, and UTF-32 stand for?
  4. Describe the key feature of UTF-8. Why is this variable-width encoding so advantageous for web content?
  5. How does UTF-32 work? What is its main advantage and its main disadvantage?
  6. The Unicode code point for the Euro sign (€) is U+20AC. Would this character require 1, 2, 3, or 4 bytes in a UTF-8 encoding? (You don't need to calculate the exact bits, just the byte count based on its range).
  7. How many bytes does the character 'A' (U+0041) occupy in UTF-8, UTF-16, and UTF-32 respectively?
  8. What is the relationship between the first 128 characters of Unicode and the standard ASCII set?
  9. Compare UTF-8 and UTF-16 in terms of space efficiency for documents containing mostly English text versus documents containing mostly East Asian characters (e.g., Chinese, Japanese).
  10. Briefly explain what "endianness" (Big-Endian vs. Little-Endian) is and why it is a concern for UTF-16 and UTF-32 but not for UTF-8.